Understanding network flows such as commuter traffic in large transportation networks is an ongoing challenge due to the complex nature of the transportation infrastructure and of human mobility. Here we show a first-principles based method for traffic prediction using a cost based generalization of the radiation model for human mobility, coupled with a cost-minimizing algorithm for efficient distribution of the mobility fluxes through the network. Using US census and highway traffic data we show that traffic can efficiently and accurately be computed from a range-limited, network betweenness type calculation. The model based on travel time costs captures the lognormal distribution of the traffic and attains a high Pearson correlation coefficient (0.75) when compared to real traffic. Due to its principled nature, this method can inform many applications related to human mobility driven flows in spatial networks, ranging from transportation, through urban planning to mitigation of the effects of catastrophic events.

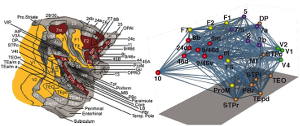
Background:The cerebral cortex is divisible into many individual areas, each exhibiting distinct connectivity profiles, architecture, and physiological characteristics. Interactions among cortical areas underlie higher sensory, motor, and cognitive functions. Graph theory provides an important framework for understanding network properties of the interareal weighted and directed connectivity matrix reported in recent studies.
Advances: We derive an exponential distance rule that predicts many binary and weighted features of the cortical network, including efficiency of information transfer, the high specificity of long-distance compared to short-distance connections, wire length minimization, and the existence of a highly interconnected cortical core. We propose a bow-tie representation of the cortex, which combines these features with hierarchical processing.
Outlook:The exponential distance rule has important implications for understanding scaling properties of the cortex and developing future large-scale dynamic models of the cortex.

Recent advances in neuroscience have engendered interest in large-scale brain networks. Using a consistent database of cortico-cortical connectivity, generated from hemisphere-wide, retrograde tracing experiments in the macaque, we analyzed interareal weights and distances to reveal an important organizational principle of brain connectivity. 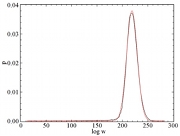Using appropriate graph theoretical measures, we show that although very dense (66%), the interareal network has strong structural specificity. Connection weights exhibit a heavy-tailed lognormal distribution spanning five orders of magnitude and conform to a distance rule reflecting exponential decay with interareal separation. A single-parameter random graph model based on this rule predicts numerous features of the cortical network: (1) the existence of a network core and the distribution of cliques, (2) global and local binary properties, (3) global and local weight-based communication efficiencies modeled as network conductance, and (4) overall wire-length minimization. These findings underscore the importance of distance and weight-based heterogeneity in cortical architecture and processing.

The mathematical structure of Sudoku puzzles is akin to hard constraint satisfaction problems lying at the basis of many applications, including protein folding and the ground-state problem of glassy spin systems. Via an exact mapping of Sudoku into a deterministic, continuous-time dynamical system, here we show that the difficulty of Sudoku translates into transient chaotic behavior exhibited by this system. We also show that the escape rate κ, an invariant of transient chaos, provides a scalar measure of the puzzle's hardness that correlates well with human difficulty ratings. Accordingly, η = - log₁₀ κ can be used to define a "Richter"-type scale for puzzle hardness, with easy puzzles having 0 < η ≤ 1, medium ones 1 < η ≤ 2, hard with 2 < η ≤ 3 and ultra-hard with η > 3. To our best knowledge, there are no known puzzles with η > 4.

Boolean satisfiability (k-SAT) is one of the most studied optimization problems, as an efficient (that is, polynomial-time) solution to k-SAT (for k > 2) implies efficient solutions to a large number of hard optimization problems. Here we propose a mapping of k-SAT into a deterministic continuous-time dynamical system with a unique correspondence between its attractors and the k-SAT solution clusters. We show that beyond a constraint density threshold, the analog trajectories become transiently chaotic, and the boundaries between the basins of attraction of the solution clusters become fractal, signalling the appearance of optimization hardness. Analytical arguments and simulations indicate that the system always finds solutions for satisfiable formulae even in the frozen regimes of random 3-SAT and of locked occupation problems (considered among the hardest algorithmic benchmarks), a property partly due to the system's hyperbolic character. The system finds solutions in polynomial continuous time, however, at the expense of exponential fluctuations in its energy function.

Betweenness centrality lies at the core of both transport and structural vulnerability properties of complex networks; however, it is computationally costly, and its measurement for networks with millions of nodes is nearly impossible. By introducing a multiscale decomposition of shortest paths, we show that the contributions to betweenness coming from geodesics not longer than L obey a characteristic scaling versus L, which can be used to predict the distribution of the full centralities. The method is also illustrated on a real-world social network of 5.5 Million nodes and 27 Million links.

Uniform sampling from graphical realizations of a given degree sequence is a fundamental component in simulation-based measurements of network observables, with applications ranging from epidemics, through social networks to Internet modeling. Existing graph sampling methods are either link-swap based (Markov-Chain Monte Carlo algorithms) or stubmatching based (the Configuration Model). Both types are ill-controlled, with typically unknown mixing times for link-swap methods and uncontrolled rejections for the Configuration Model. Here we propose an efficient, polynomial time algorithm that generates statistically independent graph samples with a given, arbitrary, degree sequence. The algorithm provides a weight associated with each sample, allowing the observable to be measured either uniformly over the graph ensemble, or, alternatively, with a desired distribution. Unlike other algorithms, this method always produces a sample, without backtracking or rejections. Using a central limit theorem-based reasoning, we argue, that for large N, and for degree sequences admitting many realizations, the sample weights are expected to have a lognormal distribution. As examples, we apply our algorithm to generate networks with degree sequences drawn from power-law distributions and from binomial distributions.

We consider the effect of network topology on the optimality of packet routing which is quantified by γ , the rate of packet insertion beyond which congestion and queue growth occurs. We show that for any network, there exists an absolute upper bound, expressed in terms of vertex separators, for the scaling of γ with network size N, irrespective of the static routing protocol used. We then derive an estimate to this upper bound for scale-free networks and introduce a static routing protocol, the "hub avoidance protocol", which, for large packet insertion rates is superior to shortest path routing.

Most mathematical models for the spread of disease use differential equations based on uniform mixing assumptions or ad hoc models for the contact process. Here we explore the use of dynamic bipartite graphs to model the physical contact patterns that result from movements of individuals between specific locations. The graphs are generated by large-scale individual-based urban traffic simulations built on actual census, land-use and population-mobility data. We find that the contact network among people is a strongly connected small-world-like graph with a well-defined scale for the degree distribution. However, the locations graph is scale-free, which allows highly efficient outbreak detection by placing sensors in the hubs of the locations network. Within this large-scale simulation framework, we then analyse the relative merits of several proposed mitigation strategies for smallpox spread. Our results suggest that outbreaks can be contained by a strategy of targeted vaccination combined with early detection without resorting to mass vaccination of a population.

We define gradient networks as directed graphs formed by local gradients of a scalar field distributed on the nodes of a substrate network G. We derive an exact expression for the in-degree distribution of the gradient network when the substrate is a binomial (Erdős-Rényi) random graph, G(N,p). Using this expression we show that the in-degree distribution R(l) of gradient graphs on G(N,p) obeys the power law R(l)~1/l for arbitrary, i.i.d. random scalar fields. We then relate gradient graphs to congestion tendency in network flows and show that while random graphs become maximally congested in the large network size limit, scale-free networks are not, forming fairly efficient substrates for transport. Combining this with other constraints, such as uniform edge cost, we obtain a plausible argument in form of a selection principle, for why a number of spontaneously evolved massive networks are scale-free.

In a parallel discrete-event simulation (PDES) scheme, tasks are distributed among processing elements (PEs), whose progress is controlled by a synchronization scheme. For lattice systems with short-range interactions, the progress of the conservative PDES scheme is governed by the Kardar-Parisi-Zhang equation from the theory of non-equilibrium surface growth. Although the simulated (virtual) times of the PEs progress at a nonzero rate, their standard deviation (spread) diverges with the number of PEs, hindering efficient data collection. We show that weak random interactions among the PEs can make this spread nondivergent. The PEs then progress at a nonzero, near-uniform rate without requiring global synchronizations.

We investigate the effects of finite size and inertia of a small spherical particle immersed in an open unsteady flow which, for ideal tracers, generates transiently chaotic trajectories. The inertia effects may strongly modify the chaotic motion to the point that attractors may appear in the configuration space. These studies are performed in a model of the two-dimensional flow past a cylindrical obstacle. The relevance to modeling efforts of biological pathogen transport in large-scale flows is discussed. Since the tracer dynamics is sensitive to the particle inertia and size, simple geometric setups in such flows could be used as a particle mixture segregator separating and trapping particles.

Hydrodynamical phenomena play a keystone role in the population dynamics of passively advected species such as phytoplankton and replicating macromolecules. Recent developments in the field of chaotic advection in hydrodynamical flows encourage us to revisit the population dynamics of species competing for the same resource in an open aquatic system. If this aquatic environment is homogeneous and well-mixed then classical studies predict competitive exclusion of all but the most perfectly adapted species. In fact, this homogeneity is very rare, and the species of the community (at least on an ecological observation time scale) are in nonequilibrium coexistence. We argue that a peculiar small-scale, spatial heterogeneity generated by chaotic advection can lead to coexistence. In open flows this imperfect mixing lets the populations accumulate along fractal filaments, where competition is governed by an "advantage of rarity" principle. The possibility of this generic coexistence sheds light on the enrichment of phytoplankton and the information integration in early macromolecule evolution.

On the nanometer scale, a seemingly smooth crystalline surface is not only bumpy, it's also in motion. Tiny mesas and depressions appear and disappear; escarpments range over the surface like waves on a beach. These thermal fluctuations are visible, thanks to advances in imaging techniques, which exploit electrons to divine the nanoscale motions. But although experiments can capture the spatial structure of surface fluctuations with atomic resolution, they lack the temporal resolution to follow the hops of individual atoms. Instead, observations yield a set of parameters that characterize how the surface changes on longer, millisecond timescales. Can these parameters be derived from physical arguments to predict the nanoscopic behavior of surfaces? With so much activity at the atomic level, building a model based on the behavior of individual atoms is too difficult. Moreover, we do not know how all the atomic degrees of freedom couple to the motion of surface features formed by tens to hundreds of atoms. Fortunately, it turns out that a thermodynamic approach - one that treats fluctuations as the larger-scale manifestations of atoms moving in equilibrium - can successfully account for the observed behavior. This approach, which is the subject of this article, has more than academic interest. As devices shrink in size to the nanometer scale, the measurement, characterization, and understanding of how tiny surface features evolve will be crucial in determining the reliability and utility of nanostructures.